THE CUT FREQUENCY

The cut frequency is so-called because it is the frequency from which a filter starts to operate the rejection of the unwanted frequency bands. Although the term cut gives the idea of something sharp, be aware that this barring isn't sudden at all, but more or less gradual depending on the filter type.

Imagine being at the cinema and seeing the sheriff get off his horse while a lap-dissolve — it's called this way — opens up on the coach running in the desert. That's exactly the way the transition happens from a band to the adjacent one by means of the crossover. The lowpass gradually gets rid of the sheriff, about whom it doesn't care anything about, while gradually the highpass brings us on the coach, which all were asking where the hell it was! Of course this rule works for other types too, as thriller and spy-story. Even in porn this technique is used — although you'll agree with us it's better to continue using the example of the sheriff. Well, why did the director choose to fade while Wyatt Earp gets off horse, and not in any other scene? (Read: how to choose the cut frequency in a speaker system?)

As a rule of thumb it can be affirmed that this has to be central compared with the frequency range that both involved speakers can play without a filter. This implicitly presupposes that the response of both speakers overlaps for a good part. Having a midbass able to rise up to 3Khz and a tweeter that goes down to 1Khz, the cut frequency could be easily located in 2Khz, a central frequency in comparison to the range that both speakers are able to play. On the contrary, a woofer that reaches 2Khz cannot be coupled with a tweeter that starts from 3Khz, under pain of strong alterations in the general response of the system.

Another aspect to be held in serious consideration is the ability of the speaker to accept power. Every speaker, of any kind, brand and quality, the more it moves the more it distorts. For the same emitted acoustic level, any diaphragm suffers an excursion as much strong as lower the frequency, distorting accordingly. To control this distortion, therefore, its crossover frequency will have to be shifted upward according to the applied power. But the energetic content of a musical signal is not constant with the frequency, so the evaluation of the power applied to a single component at a certain crossover frequency is not so immediate. For this reason we have provided you with this chart that shows the energetic distribution of the musical signal depending on the frequency:

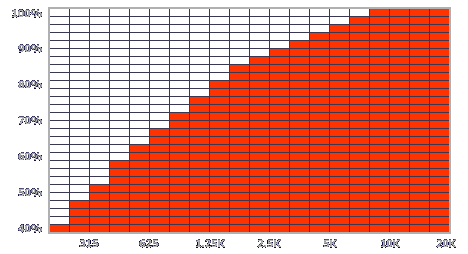
How to use it: locate a certain cut frequency on the abscissa and find its correspondent percentage value. That will be referred to lowpass. Subtract it from 100 to get the value referred to highpass. Very easy, isn't it?

But 'cause all seems not so easy, the cut frequency — or crossover frequency, as we have indifferently named it up to now — is also called -3dB frequency, and so you'll have to call it to cut a fine figure in circles that count. This eccentric name is due to the fact that it is identified as cut frequency that given back with an attenuation by 3dB compared to the average level of the wave band. The concept of wave band will be clearer after we'll have spoken of order and slope of filters