THE FILTER Q

In electrotechnics and electroacoustics the letter Q is synonymous with merit factor. The word merit can induce the more witty among you to think of a mark that distinguishes a well made filter from a badly made one, but it's not this way. The merit factor is, yes, a number, but it describes the trend of response in proximity of the cut frequency. See how, conventionally reporting to second-order filters. In the illustration below you can observe the overlapped responses of two generic highpass filters, both tuned to 100hz:

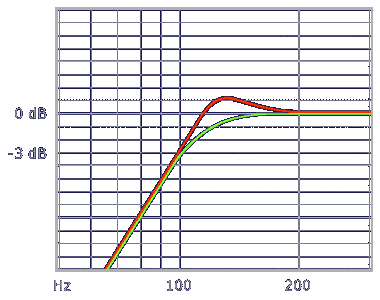
You'll notice they are evidently different, although associated by the fact they exhibit an equal attenuation slope below f_-3

According to their profile around the cut frequency the curves take a name, which is the one of the mathematician that first got its related equations. You'll hear therefore about Bessel curves, Butterworth, quasi-Butterworth, Chebyshev, all imbeciles who had their balls shaken on filters instead to go fishing. To each curve corresponds a different merit factor. For example the second-order Butterworth is characterized by a Q of .707 and is also called maximally flat because it tends more than all the others to reach the ordinate 0dB without never trespassing it — as a rule, 0dB is assumed to be the mean level of the wave band. Quasi-Butterworth and Bessel curves show merit factors lower than .707 and they too never overcome the level of the wave band. On the contrary Chebyshev and others have higher merit factors and produce a ripple more or less accented in the crossover region — particularly, the second-order Chebyshev shows a Q equal to 1.

In second-order filters the Q value is given by the ratio between the capacitor and inductor values, according to the formula

Q = Z*√(C/L*10³)

The formulas we have provided you for second-order flters are associated to Q's equal to .707 — try it, you'll see it works. It's evident however that altering C and L values also changes the filter Q. Take the second-order formulas, both lowpass and highpass, and replace the 2 under the radical sign with the integer

and you'll always get a second-order filter even though with different values of components, but with a Q of .5 related to a crossover point of -6dB. This is not a trick to force you to do some more calculations, oh no, it's the expression of a precise theoretical model known as all-pass filter — another word to write down if you wish to create a good impression with your friends.

If now you think you have finally reached the end, set your mind at rest. In solving all the formulas you would find very often that there don't exist in the marketplace components for the values you are looking for. The problem is marginal for inductors that are generally custom-made but it is decidedly felt for capacitors and in less measure for resistors. Your choices would then be two. Use a component value closest to the one resulting from calculations, but in this case it would be mandatory re-calculate the new cut frequency reversing the terms in the formulas. The other option would be to make up yourself the desired value appropriately combining two or more standard elements with series and parallel connections